Project Reality Forums

Posted: **2010-08-24 08:00**

at the moment we are looking at having 32 deployable mortars total, 16 tops for each firebase and the rate of fire we are looking at 900 rpm, going to have an invisible guy on steroids (and maybe a little more) reloading this baby

Posted: **2010-08-24 09:59**

[R-DEV]Rhino wrote:at the moment we are looking at having 32 deployable mortars total, 16 tops for each firebase and the rate of fire we are looking at 900 rpm, going to have an invisible guy on steroids (and maybe a little more) reloading this baby

Sounds amazing. Can it teleport people around the map and enable fast-ropes too?

Posted: **2010-08-24 11:08**

The video is pretty awesome! Can't wait to use those ingame someday!

how could I miss this for so long... isn't that worth a post in the newssection? or did I miss it there too?

Posted: **2010-08-24 11:28**

there are also posts in the news section ...

Posted: **2010-08-24 11:36**

I've got a tutorial video that I may post up sometime if I get the go.

Posted: **2010-08-24 12:12**

Wilkinson wrote:Range = -8.869232072*10^(-22)*x^8 + 5.863078464*10^(-1 *x^7 - 1.645660969*10^(-14)*x^6 + 2.552955503*10^(-11)*x^5 - 2.385872722*10^(- *x^4 + 1.370373343*10^(-5)*x^3 - 4.712480004*10^(-3)*x^2 + 8.691949397*10^(-1)*x + 19.70789909 WHICH Equals....

swoop da woop.
Still amazing stuff done. A gary variant would be amazing. As well as a Stryker Varient

What do all those numbers indicate? Are those constants used in game's engine or did you calculate them?

Well, what i'm wondering is did you come up with those numbers or you just made an equation using engine's various (gravity etc) known values?

PS: I know nothing about modding, just trying to figure out how it works.

Posted: **2010-08-24 13:44**

Seriously lol'd at; "POOF!" exits vehicles runs to car and drives at 500kph to marker xD

Posted: **2010-08-24 14:40**

It looks great! I'm looking forward to see how it effects the battle! It surly is a good job in any way.

However, I've watched your previous mortar-vid, and somehow I like that sighting system better. How come you have changed it?

Posted: **2010-08-25 13:52**

Wow, that is some great work. I'd love to see these in-game and I'm even more interested in how tactics will adapt to use and counter them.

Posted: **2010-08-26 22:03**

So true. I think it will all depends on how much each team can use them. To much, and they will ruin the gameplay in many ways I think.
BUT, in DEV's we trust. Think 0,95 will be awesome!

Now I just have to get that new computer...

I've been missing the mortar since the day vBF2 got released

Posted: **2014-02-08 18:51**

Hey, this looks like a necrobump, but i didn't find any newer info on this. Is it still correct with 1.1?

[quote=""'[R-DEV"]Sniperdog;1350445']Yep

Adding devation is very easy and its really up to the devs. You have a good point, IRL the M252 is actually extremely accurate, but then again IRL it is no where near as easy to get range with an accuracy of 1m, not to mention things like wind.

The actual physics equation came out to:
Angle = 90 - sin^-1 (-14.70235*Range/(projectile velocity)^2)/2.
Where -14.7 is the acceleration due to gravity in BF2 (with the gravity modifier set to 1)

This allowed me to compute the maximum range just fine but for some reason it didn't work correctly with some of the other angles.

The equation I modeled after doing some measurements is:

Range = -8.869232072*10^(-22)*x^8 + 5.863078464*10^(-1

*x^7 - 1.645660969*10^(-14)*x^6 + 2.552955503*10^(-11)*x^5 - 2.385872722*10^(-

*x^4 + 1.370373343*10^(-5)*x^3 - 4.712480004*10^(-3)*x^2 + 8.691949397*10^(-1)*x + 19.70789909

where x is the range. This equation worked to an accuracy of within about 2 meters.

This equation is only really useful to angles for this weapon though

[/quote]
[quote="Wilkinson""]Range = -8.869232072*10^(-22)*x^8 + 5.863078464*10^(-1

*x^7 - 1.645660969*10^(-14)*x^6 + 2.552955503*10^(-11)*x^5 - 2.385872722*10^(-

*x^4 + 1.370373343*10^(-5)*x^3 - 4.712480004*10^(-3)*x^2 + 8.691949397*10^(-1)*x + 19.70789909 WHICH Equals....

swoop da woop.
Still amazing stuff done. A gary variant would be amazing. As well as a Stryker Varient

[/quote]

'[R-DEV wrote:Sniperdog;1351094']The problem is for some reason the equations don't correlate precisely with the in game results. The eqation to use should be

θ = asin(Rg/v^2)/2

But for some reason it doesn't give me perfect results. I at first thought It might be that my hud was off or that I wasn't being precise enough, but that was until I noticed there was even a pattern to the error between the measured and ballistics equation results.

R-------θ (meas)---θ(calc)------error

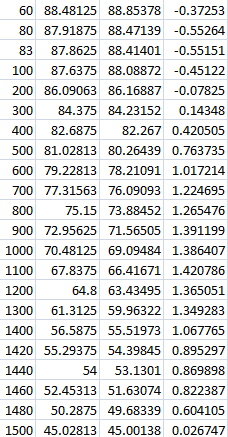
As you can see for some reason the angles in the middle between 45 and 90 seem to have a higher degree of inaccuracy. I basically have already fixed this problem (as you can see in the vid) by simply measuring the major values and then using regression.

I made an table with this formula:

Rincewind The Wizzard, post: 73169, member: 145 wrote: velocity = 121.306;
gravity = 9.81;
winkeltan = (Math.pow(velocity,2) + Math.sqrt(Math.pow(velocity,4) - gravity * (gravity * Math.pow(range,2)+ 2 * height_difference * Math.pow(velocity,2))))/(gravity * range);
winkel = Math.atan(winkeltan) * 180/Math.PI;
mils = winkel / 0.05625;
mils = mils.toFixed(0);
angle = winkel.toFixed(2);

smth like that. There is also mortarcalc based on ImageJ scripts somewhere on the PR forums (search for SkyJumpy) you can look at it's code

Here's my table:

The formula is:

Code: Select all

=(POWER(121,306;2)  + SQRT(POWER(121,306;4) - 9,81 * (9,81 * POWER(A2;2) + 2 * B2 *  POWER(121,306;2)))) / (9,81 * A2)

Here's hidden columns showing calculation steps:

And the "old" table (we used that in eg. in PRWC):

As one can see, there's some deviation with calculated range when compared with the "old" table (which i have no idea how calculated). Moreover small deviation with ingame calculator giving 1481 for 350m and this calculation gives 1480,0599...

Would be nice to know, if this calculation gives just more exact output? Is this confirmed as the formula PR 1.1 uses? And does this amount of deviation have any significance at all?

Posted: **2014-02-10 21:52**

As one can see, there's some deviation with calculated range when compared with the "old" table (which i have no idea how calculated). Moreover small deviation with ingame calculator giving 1481 for 350m and this calculation gives 1480,0599...

Would be nice to know, if this calculation gives just more exact output? Is this confirmed as the formula PR 1.1 uses? And does this amount of deviation have any significance at all?

There is almost no significance in the error,

for discussion ... looking from a top down map view, the "cone of fire" for the mortars are a 10meter radius, 20 meter diameter, and even at 1500m the rounding errors provide a simulated real world rate of error. It's about as accurate as we want to get it.

Project Reality Forums

[Code] Deployable Mortar (M252 81mm)

Re: [Code] Deployable Mortar (M252 81mm)

Re: [Code] Deployable Mortar (M252 81mm)

Re: [Code] Deployable Mortar (M252 81mm)

Re: [Code] Deployable Mortar (M252 81mm)

Re: [Code] Deployable Mortar (M252 81mm)

Re: [Code] Deployable Mortar (M252 81mm)

Re: [Code] Deployable Mortar (M252 81mm)

Re: [Code] Deployable Mortar (M252 81mm)

Re: [Code] Deployable Mortar (M252 81mm)

Re: [Code] Deployable Mortar (M252 81mm)

Re: [Code] Deployable Mortar (M252 81mm)

Re: [Code] Deployable Mortar (M252 81mm)